마인크래프트 스피드런 유튜버 '드림' 치트 사건으로 알아보는 통계

내용에 앞서

이 포스팅은 드림이 나쁘다 아니다 이런 것을 따지기 위해 작성된 게 아니라, 스피드런 관리팀이 어떻게 그가 치트를 썼다고 확신했는지, 그 과정에서 어떠한 통계적 검증을 사용했는지 순수하게 수학적, 통계적, 컴퓨터공학적 관점에서 이 사건이 흥미로웠기 때문에 스피드런 관리팀이 사용한 통계적 검증 방법에 대해 설명하는 포스팅입니다.

 

이 포스팅의 내용은 다음과 같은 영상 및 자료를 기반으로 작성되었습니다.

• (영상) [Dream cheating scandal - explaining ALL the math simply] by  Mathemaniac
• (영상) [Did Dream Fake His Speedruns - Official Moderator Analysis] by Geosquare
• (PDF) [Dream Investigation Results] by Official Report by the Minecraft Speedrunning Team
• (영상) [How lucky is too lucky?: The Minecraft Speedrunning Dream Controversy Explained] by Stand-up Maths

또한 필자는 통계학을 전공한 적은 있지만 중간에 공대로 전과하였고, 통계를 손절한지 어연 7년이 되어가기 때문에 내용에 잘못 설명한 부분이나 오류가 있을 수 있습니다.

 

서론

제가 최근에 마크 스피드런에 관심을 가지게 되면서 이 영상 저 영상을 많이 보다보니 유튜브에 관련 영상들이 많이 뜨는데 이목을 끄는 영상이 있었습니다.

 

'드림'의 스피드런을 조작으로 판결내린 이유에 관한 speedrun.com 공식 관리자의 영상이었습니다.

드림이라는 인물에 대해서도 잘 알고 있었고, 최근엔 취미로 스피드런을 배우고는 있지만 처음에 이 영상 썸네일을 보곤 "아니 얘가 스피드러너였어?"라는 생각(...)이었습니다.

애초에 저는 드림 영상은 맨 헌트 시리즈(드림 vs 친구 5명의 대결 구도로 드림은 엔더 드래곤을 잡아야하고, 친구들은 이를 방해해서 드림을 1번이라도 죽이면 승리하는 시리즈)만 정주행했었고, 스피드런에 관심을 가지게 된 계기는 드림이 아니라 Brentilda의 영상 때문에 스피드런에 입문한 거였어서 드림이 스피드러너일 거라곤 생각도 안 하고 있었기 때문이죠.

 

잘하는 배그 유튜버는 많지만 그 중에서 프로를 하는 사람은 드물기 때문에 처음보는 배그 유튜버가 잘한다고 해서 '이 사람은 프로게이머인가봐'라고는 보통 잘 생각 안 하는 것과 같은 맥락이었죠.

 

드림Dream?

드림이란 어떤 사람인가하면 그냥 마크를 잘하는 사람입니다. 그런데 특출나게 잘하는 편이죠.

지옥문에서 나오자마자 상대팀의 용암 함정에 빠지고 -> 그 용암 공격을 바로 물로 상쇄시켜버렸지만 -> 상대팀이 바로 물을 빼앗아 버렸고 -> 그리고 밀어서 떨어뜨렸는데 -> 떨어지는 중에 아래에 말이 있다는 걸 확인하고 -> 말은 맨손으로만 탈 수 있으니까 손에 있던 칼을 공중에서 던져버리고 -> 말에 탑승해서 낙하 데미지를 없애버리는 짤입니다.

 

드림의 가장 유명한 장면이죠.

공중에서 상대방이 밀쳐서 떨어지는데 -> 중간에 크래프팅 테이블이 있다는 걸 확인하고 -> 크래프팅 테이블을 열고 -> 인벤토리에서 나무 목재를 찾아서 -> 보트를 조합하고 -> 보트가 5번 슬롯에 들어갔다는 걸 확인하고 -> 5번 슬롯으로 변경한 후 -> 바닥에 닿기 직전에 보트를 설치하고 -> 다시 또 바닥에 닿기 직전에 보트에 타서 낙하 데미지를 없애는 그야말로 입으로나 가능할 법한 플레이를 보여주었죠.

 

하도 현실성이 떨어져서 짜고 해당 클립을 만들어내기 위해 상황을 연출한 게 아니냐는 의심도 많이 받아서 무편집 풀영상도 공개되어 있는 영상입니다.

 

상당히 인상 깊은 플레이임은 분명하지만 이런 맨헌트 영상들이 조작이냐 아니냐는 이번 포스팅의 주제가 아닙니다.

 

드림 스피드런 치트 의혹의 시작

드림은 예전에 스피드런 랭커이기도 했는데 여기서 다른 스피드러너들에 비해 드림만 특정 아이템의 드랍률이 말도 안 되게 높다는 의혹이 나왔습니다.

바로 엔더 진주와 블레이즈 막대죠.

엔더 진주

 

블레이즈 막대

 

블레이즈 막대는 '블레이즈'를 잡을 때 50% 확률로 드랍되는 아이템입니다.

엔더 진주는 '엔더맨'을 잡을 때 확률적으로 드랍되는 아이템인데 스피드런에서는 엔더맨을 잡아서 엔더진주를 획득하지 않습니다. 엔더맨 스폰 확률이 너무 낮기 때문에 엔더맨을 직접 잡아서는 빠른 기록을 세울 수 없기 때문입니다. 그렇기에 '피글린'에게 금을 주고 확률적으로 엔더 진주를 획득하는 '물물교환' 시스템을 이용해서 엔더 진주를 획득합니다.

 

물물교환에서 금 1개를 주었을 때 엔더 진주를 얻을 확률은 정확히 42/262 입니다.

쉽게 말해 엔더 진주를 얻을 확률은 대략 5% 입니다. (마인크래프트 최신버전의 확률(약 2%)과 다릅니다. 마크 스피드러너들은 엔더 진주 확률이 가장 높은 1.16.1 버전에서 플레이하며, 드림이 플레이한 버전도 이 1.16.1 버전입니다.)

 

 

드림은 스피드런 기록을 세울 때 생방송을 같이 진행하면서 기록을 세웠는데 그때 드림이 블레이즈 막대와 엔더 진주를 획득한 확률은 다음과 같습니다.

 

	드림의 성공 횟수 / 시도 횟수	드림의 확률	원래 확률
엔더 진주	42/262	약 16%	약 5%
블레이즈 막대	211/305	약 69%	50%

 

저는 처음에 이거 보고는 5%에서 16%? 그리고 50%에서 69%?

11%p, 19%p 차이 정도는 운이 좀 좋으면 충분히 나올 수 있는 수치 아닌가...? 싶었습니다.

 

아니 솔직히 그렇지 않나요? 5% 확률의 엔더 진주가 막 60% 확률로 나오고 그러면 "와 이건 빼박 치트인데?" 싶어도 5%가 16%...? 이게 과연 치트인가? 싶은 느낌이 듭니다.

 

하지만 통계라는 것은 '사람의 직관으로 생각했을 때와 실제 확률이 엄청나게 괴리가 큰 경우'가 종종 있습니다.

이런 경우의 대표적인 예시로 생일 패러독스가 유명합니다.

한 학급에 30명의 학생이 있을 경우, 직관적인 생각으로는 이 30명 중에 생일이 겹치는 학생이 아무도 없을 가능성이 훨씬 높을 것이라고 생각합니다.

 

1년이 365일인데 30명 중에서 생일이 겹치는 건 엄청 드문 게 아닌가?

 

하지만 실제로 계산해보면 생일이 겹치는 사람이 있을 확률이 70.63%로 훨씬 높습니다.

(https://blog.naver.com/alwaysneoi/220261751961)

 

이처럼 실제 확률이 직관과는 모순되는 경우가 종종 있습니다.

그래서 스피드런 페이지 관리자팀원들은 '드림처럼 엔더 진주가 16% 확률로, 블레이즈 막대가 69% 확률로 드랍될 확률이 얼마인가?'를 수학적으로 계산하였습니다.

 

관리자팀이 설명하는 증명 과정이 정말 흥미로웠습니다.

스피드런 페이지 관리팀이 작성한 'Dream Investigation Results' 일부

통계학 대학원생이 석사 과정 논문으로 제출했다고 해도 믿을 정도로 자세하고 (비록 최초 계산 확률에 오류가 있어서 수정 작업을 하였지만) 꽤 엄밀하게 29장에 걸쳐서 왜 드림이 치트를 썼다고 결론을 내렸는지에 대해 보고서Dream Investigation Results를 작성하였습니다.

 

아마 제가 대학생때 통계를 이런 재미있는 예시로 배웠더라면 통계는 나랑 안 맞는다면서 때려치우고 통계학과에서 전과하는 일도 없었을지도 모르겠습니다.

 

드림 정도의 운을 가지려면 상위 몇 퍼센트의 인간이어야 하는가?

수능 1등급은 상위 4%입니다.

롤 챌린저는 상위 0.003% 입니다.

전 세계에서 1위 부자인 일론 머스크는 상위 0.0000000126029727% 입니다. (79억(인구 수) 분의 1)

그러면 드림의 엔더 진주 & 블레이즈 막대 운은 상위 몇 퍼센트일까요?

 

스피드런 관리자팀의 계산에 따르면 드림의 운은
상위 0.00000000001325504% 입니다.

0.00000000001325504%는 분수로 표현하면 다음과 같습니다.

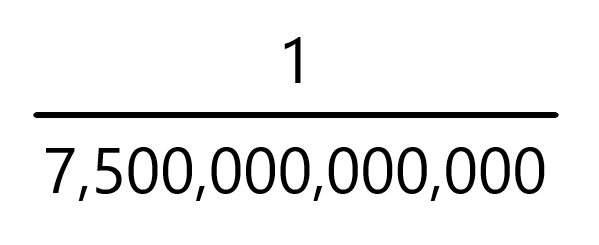
7조 5천억분의 1 확률입니다.

 

현재까지 지구상에 태어난 적이 있는 모든 인간을 합쳐도 1082억 명이라고 합니다. (https://zdnet.co.kr/view/?no=20170524095423)

 

우리가 살고 있는 지구 상의 인류가 전부 예토전생해서 무덤에서 부활한다고 쳐도 택도 없는 숫자입니다.

 

75개의 평행 우주에서 존재하는 지구를 가져와서 75개의 지구에 살았던 사람들을 다 부활시켜도 그 중에 이 정도 운을 가진 사람이 1명 있을까 말까한 확률입니다.

 

어벤져스 인피니티워에서 닥터 스트레인지가 타노스와 싸울 때 1400만 개의 미래를 보았지만 그 중 단 1개의 승리 시나리오만 존재했다며 거기에 베팅을 했었죠.

 

1400만 분의 1 확률이니까 그나마 베팅했지 만약 7조 5천억 분의 1 확률이었으면 그냥 그 자리에서 항복하고 타노스 밑에서 일하는 충실한 부하가 되었을 것 같습니다.

 

드림의 엔더 진주(16%)와 블레이즈 막대(69%) 확률에서 어떻게 계산해야 7조 5천억 분의 1(0.00000000001325504%)이 나온 걸까?

스피드런 관리팀(이하 관리팀)은 그럼 어떤 계산을 해서 7조 5천억 분의 1이 나온 걸까요?

관리팀은 p-value라고 불리는 통계적 검증 방법을 사용했습니다.

 

p-value는 쉽게 말해 '치트를 쓰지 않았다고 가정할 경우, 그 사람이 262번의 피글린 물물교환에서 42번의 엔더 진주를 얻고, 305번의 블레이즈 처치에서 211개의 블레이즈 막대를 얻을 확률이 얼마나 되는가?'를 계산하는 방법입니다.

 

치트를 쓰지 않았다는 가정을 깔고 시작했을 때 실제로 발생할 확률이 말도 안 되게 낮다면 그건 가정이 틀렸다는 이야기이다라는 논리를 이용하여 가설을 검증하는 방식입니다.

관리팀에서 계산한 '262번 중 42번의 엔더진주, 305번 중 211번의 블레이즈 막대를 얻을 확률(p-value)'이 아까 보셨던 7조 5천억 분의 1(= 0.0000000000001325504) 입니다. (이 p-value를 어떻게 계산하는지는 뒤에서 말씀드리겠습니다.)

보통 통계학에서 이 p-value가 0.05보다 낮으면 가정이 틀렸다라고 판단합니다. 이 0.05를 보통 '임계값'이라고 합니다.

 

근데 드림의 경우 임계값인 0.05보다 훨씬 낮은 0.0000000000001325504가 나온 것이죠.

그러므로 드림은 의심의 여지 없이 '치트를 쓰지 않았다라는 가정이 틀렸다' = '드림은 치트를 썼다.'라고 관리팀에서 판단한 것이죠.

 

여기서 아까 처음 설명할 때 일론 머스크를 예로 들며 상위 0.000000000126029727의 부자라고 하여 p-value에 대해 헷갈릴 수도 있으실 것 같습니다. '아니 그럼 일론 머스크는 임계값 0.05보다 훨씬 낮으니까 일론 머스크가 부자라는 건 거짓말이라는 거야?'라고 생각할 수도 있을 것 같습니다. p-value에 대해서 약간 소개해드렸으니 이제 백분율과 p-value의 차이점에 대해서 알려드릴 때가 된 것 같습니다. 일론 머스크의 0.000000000126029727는 단순히 '일론 머스크는 79억 인구 중 1위 부자니까 1 나누기 79억을 한 백분율'이고 드림의 0.0000000000001325504는 백분율이 아니라 (아직 알려드리지 않은 복잡한 수식을 이용해 계산한) p-value입니다. 애초에 일론 머스크의 0.000000000126029727라는 숫자를 계산할 때 '일론 머스크가 돈 복사 버그를 쓰지 않았다고 가정했을 때 2160억 달러의 재산을 가지고 있을 확률은 얼마인가?'를 계산한 게 아니라는 이야기이죠. 드림의 0.0000000000001325504라는 숫자가 p-value가 뭔지 모르는 일반인들에게 얼마나 터무니 없는 수치인지 쉽게 설명하기 위해 p-value를 마치 백분율인 것처럼 함께 비교해서 '드림은 상위 몇 퍼센트의 운을 가지고 있는 사나이인가?'로 소개하였지만 p-value와 백분율은 다릅니다. (근데 애초에 스피드런 관리팀 멤버가 자기 영상에서 이렇게 비유해서...) 따라서 드림의 0.0000000000001325504라는 확률은 드림이 상위 0.00000000001325504%의 행운을 가진 사나이라는 게 아니라 그저 '드림이 치트를 쓰지 않고 엔더 진주와 블레이즈 막대를 그렇게 잘 얻을 확률'이 0.00000000001325504%라는 것입니다. 드림이 상위 몇 퍼센트의 행운을 가진 사나이인가?라고 한다면 사실 그에 대한 계산은 훨씬 쉽습니다. 마인크래프트 유저 중에서 그 누구도 드림처럼 엔더 진주와 블레이즈 막대를 획득하지 못했으므로 그는 전세계 마크 유저 중 1위이며, 전 세계 마크 유저가 약 1억 3100만 명이므로 드림은 1억 3100만 분의 1의 사나이, 즉 상위 0.000000769230769%의 백분율입니다. 정리하자면 백분율은 단순히 '나의 등수 / 전체 수'를 한 값이고 p-value는 '어떤 가정을 세웠을 때 그 일이 발생할 확률' 값입니다. 우연히 둘 다 0.0~1.0 사이의 값을 가질뿐 어떠한 관계도 없습니다. + 혹시나 해서 갑자기 덧붙여 추가하는데 0.001이라는 확률은 퍼센트로 표기하면 0.1%인 거... 아시죠? 본 포스팅에서 그냥 확률 표기랑 퍼센트 표기를 병행해서 표기하는데 헷갈리지 않게 주의 바랍니다. %가 붙으면 앞에 0이 2개 사라집니다.    0.0000000000001325504 = 0.00000000001325504%

 

그래서 p-value가 어떻게 계산하는 건데?

제가 여러분한테 동전을 하나 줍니다. 그러면서 제안을 하나 하죠.

 

 

"이 동전에는 정~~~~~말 아~~~~~무 장치도 하지 않아서 완~~~~~~전 공정하게 50% 확률로 앞면, 50% 확률로 뒷면이 나오는 절대 공평 동전이에요 ㅎㅎㅎㅎ ^^
이 동전을 던지셔서 앞면이 나오면 제가 그쪽한테 100억을 드릴게요."

그러면 여러분들은 매우 찜찜해하며 이렇게 묻겠죠. '그... 뒷면이 나오면 어떡하는데요? 저는 100억을 그쪽한테 드릴 수 없는데요?'

 

그럼 저는 대답합니다.

동전의 뒷면이 나오면 그냥 저한테 뺨따구를 야구 빠따로 한 대 맞으시면 됩니다 ^^

 

누가봐도 수상한 티가 나기 때문에 여러분들은 이 동전이 '정말 반반 확률을 가진 절대 공평 동전이 맞는지' 검증하기 위해서 내기는 하지 않고 먼저 동전만 받아서 혼자 연습삼아 1000번 던져봅니다.

 

1000번을 던져봤는데 앞면이 10번이 나오고 뒷면이 990번이 나왔습니다.

여러분들은 이 동전이 공평해보이시나요? 아니죠. 딱 봐도 앞면이 나올 확률이 1%고 뒷면이 나올 확률이 99% 정도 되는 사기 동전입니다.

 

그럼 여러분들은 저한테 따지겠죠.

 

"아니 이거 제가 1000번 던져봤더니 앞면이 딱 10번 나오는데요? 이거 앞면 나올 확률 1% 밖에 안 되는 동전이죠? 사기잖아요!"

 

그러자 저는 절대 공평 동전은 다시 탁 뺏어가며 이렇게 말합니다.

 

"그건 고객님이 방금 유독 운이 안 좋아서 그런 거예요. 아니 진짜로 우린 50% 확률인 절대 공평 동전을 드린 거라니까? 앞면 나올 확률이 1%라는 건 고객님의 뇌피셜일 뿐이잖아요~ 아니 방금만 운이 정말 안 좋았던 걸 수도 있잖아요 그죠? 반박하실 거면 증명을 해보시든가~"

 

여러분들이 정말로 운이 더럽게 안 좋아서 앞면이 딱 10번만 나올 걸 수도 있습니다.

그걸 가지고 이 절대 공평 동전의 앞면 확률이 1%라고 단정짓기는 비약이 있습니다.

어디까지나 여러분들이 1000번 던져서 10번 앞면이 나왔으므로 앞면이 나올 확률이 1%라는 것은 여러분들의 경험에 의한 '백분율'일 뿐이지 실제 동전의 확률이 얼마인지는 저만 알 수 밖에 없습니다.

 

그래서 여러분들은 이 동전의 앞면 확률이 1%라는 사실은 확신할 수 없습니다.

 

그렇다면 최소한 이 동전의 앞면이 나올 확률이 50%는 확실히 아니다라고는 증명할 수 있다면요?

앞면이 1%인지 2%인지 10%인지 뭔지는 모르겠지만 아무튼 확실히 이 사람 말처럼 절대 공정한 절대 공평 동전은 아니라는 사실은 증명할 수 있다면요?

그럼 여러분들의 눈 앞에서 동전을 뺏어들고 히죽히죽 웃고 있는 저를 사기죄로 깜빵에 충분히 넣을 수 있지 않을까요?

 

저를 깜빵에 집어넣기 위해 이 절대 공평 동전의 p-value를 계산해봅시다.

 

p-value엔 가정을 깔고 시작한다고 했죠?

여기서 가정은 다음과 같습니다.

 

가정) 이 동전은 매우 공평하여 앞면과 뒷면이 각각 무조건 50% 확률로 나온다.

 

우선 절대 공평 동전을 1000번 던졌는데 그 중 처음 10번 연속으로 앞면이 나오고 나머지 990번이 연속으로 전부 뒷면이 나올 확률은?

 

제 말에 따르면 분명 앞면이 나올 확률과 뒷면이 나올 확률은 둘 다 1/2이라고 했으므로

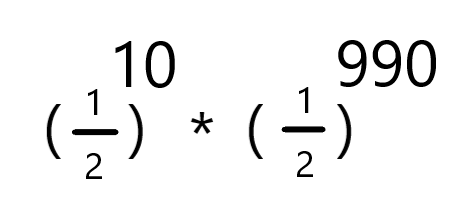
이 됩니다.

 

값을 계산해보면

0.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000093326

입니다.

 

매우 작죠. 따라서 앞뒷면 확률이 반반인 동전을 누군가 던졌을 때 딱 앞면이 연속으로 10번 나온 후 그 다음 전부 990번 뒷면이 나올 확률은 '지나가던 고양이가 갑자기 벼락을 맞았는데도 살아남은 후에 우리 집으로 펄쩍 뛰어들어온 후 제 키보드 위에서 갑자기 탭탠스를 막 췄는데 정확히 메모장에 애국가 1절부터 4절까지 적혀있어서 너무나 신기한 나머지 제가 그걸 동네방네 소문을 내려고 밖에 나갔는데 길 앞에 버려진 로또 번호가 있어서 주워서 돌아왔는데 그게 하필 로또 1등이라서 인생 역전을 할 확률'보다 낮습니다.

 

그런데 앞면이 10번 나오는게 이 경우만 있는게 아니죠.

앞 앞 앞 앞 앞 앞 앞 앞 앞 뒤 앞 뒤 뒤 뒤 뒤 뒤... (생략)

앞 앞 앞 앞 앞 앞 앞 앞 뒤 앞 앞 뒤 뒤 뒤 뒤 뒤... (생략)

앞 앞 앞 앞 앞 앞 앞 뒤 앞 뒤 앞 뒤 뒤 앞 뒤 뒤... (생략)

등 정말 많습니다.

 

그리고 각 경우는 각각 전부 확률이 

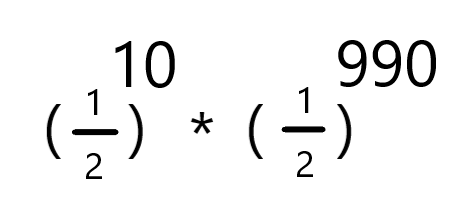
로 동일합니다.

 

어차피 곱셈 자체는 교환법칙이 성립하니까요.

 

이렇게 순서 상관 없이 1000개의 동전 중 10개만 앞으로 놓는 경우의 수는 그럼 총 몇 개가 있을까요?

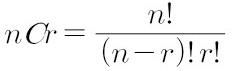
다행히 해당 경우의 수를 일일이 셀 필요 없이 위와 같은 공식이 있습니다.

위에서 n은 1000이고 r은 10입니다.

 

그럼 공식은 다음과 같죠.

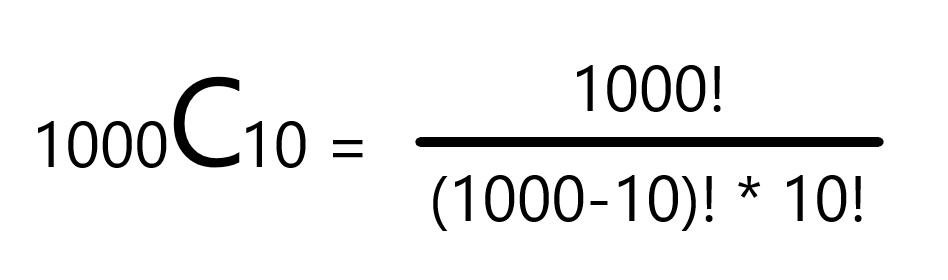
참고로 저 그림의 왼쪽에 있는 1000C10은 고등학교 수학 과정에선 저렇게 많이 쓰는데 실제 통계쪽에서는 아래와 같이 많이 씁니다.

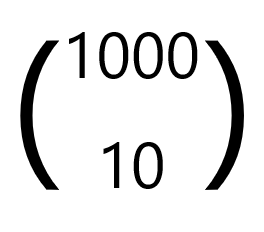
1000C10이나 이거나 똑같은 말입니다. 보통 통계학 쪽에선 이걸 주로 쓴다고 보시면 됩니다.

하지만 저는 통계학과에서 빤스런하고 공대로 전과 때려버린 통계계의 이단아이므로 1000C10이라고 쓸 겁니다.

 

아무튼 동전 1000개 중 10개만 앞면인 경우의 수는 총 1000C10 = 263,409,560,461,970,212,832,400개 입니다.

2634해 956경 461조 9702억 1283만 2400개네요.

 

동전 1000개 중 10개만 앞면인 경우의 수가 2634해 956경 461조 9702억 1283만 2400개이고, 그 경우가 모두 확률이

0.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000093326

이므로 둘을 곱하면

 

0.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000002458296

입니다.

 

따라서 확률이 반반이라 가정했을 때 1000번을 던져서 정확히 앞면이 10번만 나올 확률은

0.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000002458296

입니다.

 

하지만 이 값이 p-value는 아닙니다.

예를 들어서 1000번 중에 500번 앞면이 나왔다고 해봅시다. 딱 절반 앞면이 나왔으니까 이 동전은 정말 공평한 동전일 가능성이 높겠죠.

그런데 1000번 중에서 '딱 500번만' 앞면이 나올 가능성은

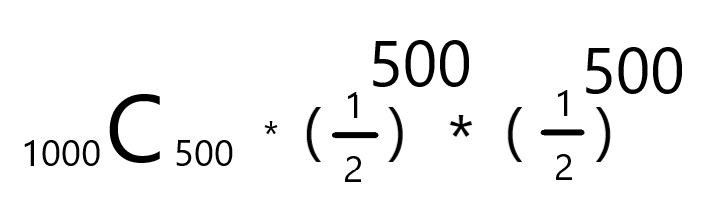
이므로 계산해보면

0.0252250181783609이 나옵니다.

퍼센트로 해보면 2.52250181783609%죠.

그럼 1000번 중에 500번이나 앞면이 나왔는데 이 동전이 진짜 공평 동전일 확률이 2.52250181783609% 밖에 안 될까요?

아닙니다. p-value는 앞면이 500번 나올 확률, 501번 나올 확률, 502번 나올 확률, 503번 나올 확률, ... , 999번 나올 확률, 1000번 나올 확률을 쭉~다 더한 값이 p-value입니다.

 

이 움짤은 1000번 중 10번이 아니라 10번 중 6번이 나왔을 때 공정한 동전일 p-value를 구하는 예시입니다.

 

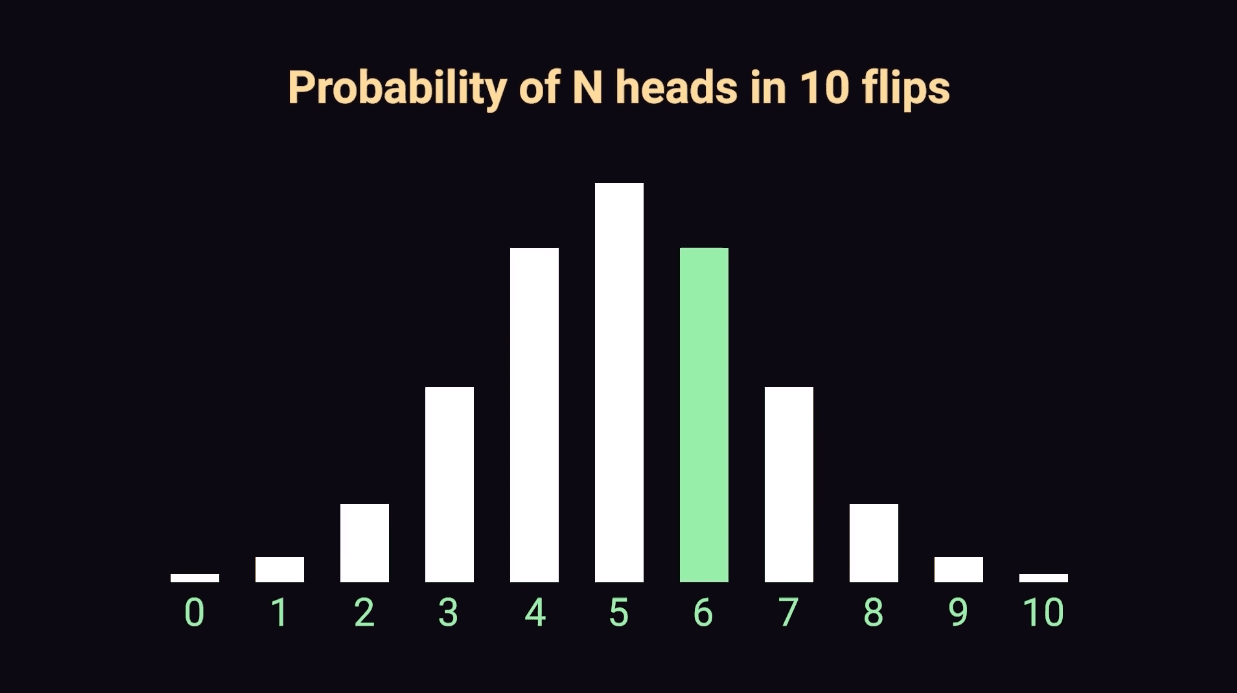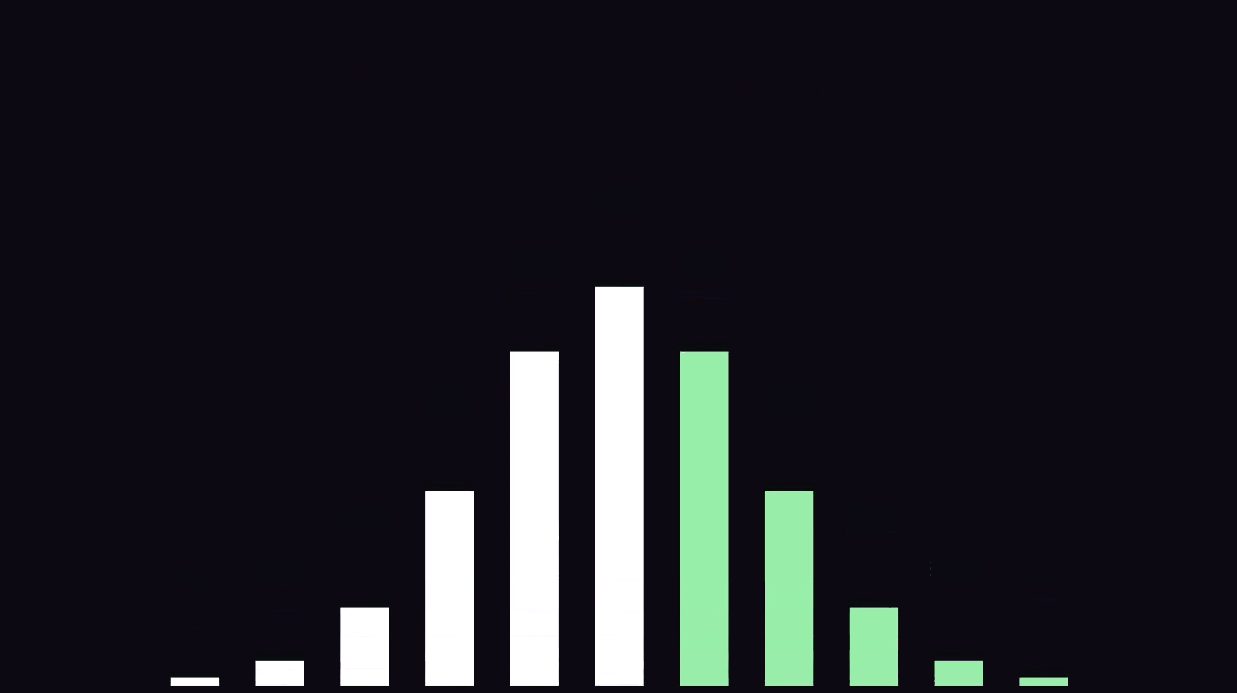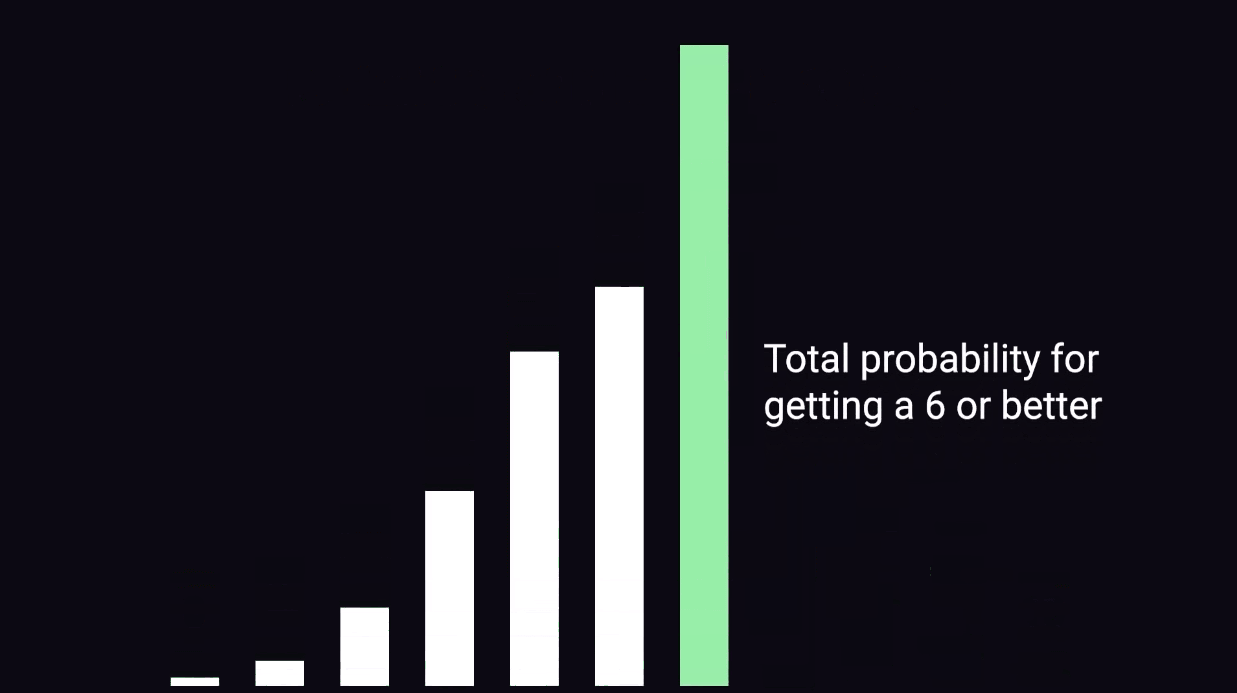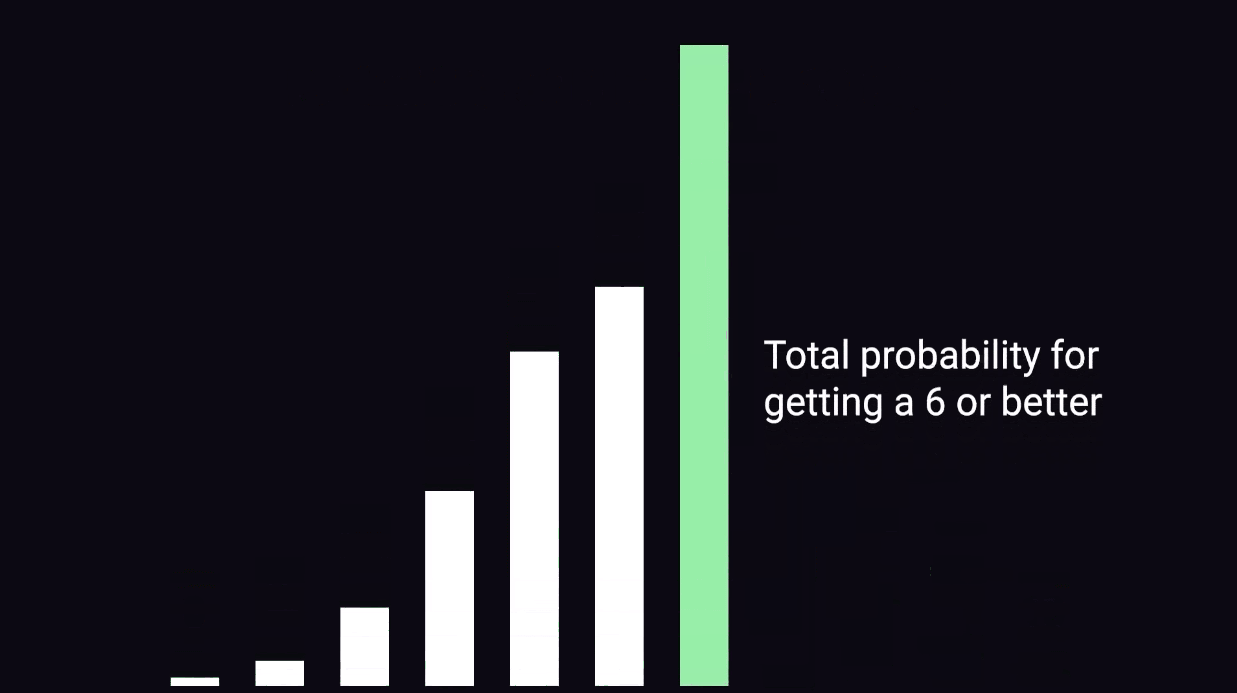
다시 앞면이 10번 나왔을 때의 p-value로 돌아가자면, 이때의 p-value는 10번만 나올 확률 + 9번만 나올 확률 + 8번만 나올 확률 + ... + 1번만 나올 확률 + 0번 나올 확률을 다 더한 값입니다.

 

그리고 그 값은
0.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000024833

입니다.

 

따라서 여러분들이 제가 드린 절대 공평 동전을 받아서 1000번 던져 봤는데 10번만 앞면이 나왔다는 것은, p-value가

0.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000024833

이라는 것이고

이는 임계값 0.05보다 한참 못 미치는 수준의 결과이기 때문에 제가 드린 절대 공평 동전은 사실 절대로 반반의 확률을 가진 공정한 동전일리 없다는 것을 증명할 수 있습니다.

 

다시 엔더 진주 이야기로 돌아와서

아까 1000번의 동전 던지기 중 10번만 앞면이 나올 확률을

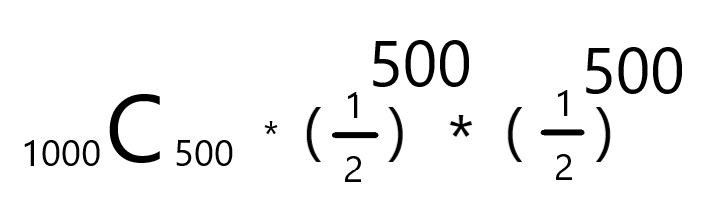
라고 했습니다.

 

이걸 일반화해서 생각해보면

가 됩니다.

 

엔더 진주의 경우를 생각해보죠.

엔더 진주의 원래 성공 확률은 0.05

엔더 진주의 원래 실패 확률은 0.95

드림의 시도횟수는 262

드림의 성공횟수는 42

입니다.

 

계산 결과는 약 0.0000000025424 입니다. (아직 p-value 아니예요! 정확히 42개만 나올 확률입니다!)

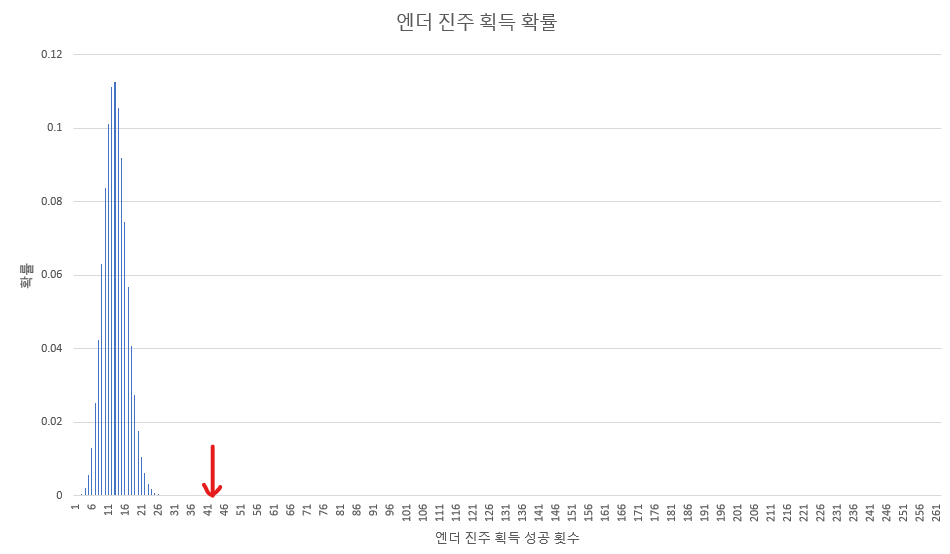
그래프 모양을 보시면 성공횟수가 13 정도일 때가 가장 높이가 높죠?

총 시도 횟수 261번 중에 엔더 진주가 원래 드랍될 확률이 5%니까 261 * 0.05 하면 13.05니까 상식적으로 생각해봐도 261번 시도하면 엔더진주는 13번 정도만 나오는 게 가장 평균적입니다.

 

13을 기준으로 멀어질수록 점점 확률이 낮아지기 시작하죠.

그래프 모양을 보면 성공횟수가 26 정도만 되어도 사실상 확률이 0%에 매우 가깝다는 걸 알 수 있습니다.

30부터는 뭐 아예 보이질 않는 수준이구요.

 

그런데 드림은 261번의 교환 시도 중에서 41번을 성공해냈습니다.

그리고 위 사진의 화살표 표시를 보다시피 41은 거의 확률이 0에 가깝습니다.

그런데 그건 딱 41번만 성공할 확률이니까 p-value가 아니죠?

 

p-value는 41번 성공부터 42번 성공, 43번 성공, ..., 261번 성공할 확률을 다 더해야합니다.

그걸 다 더했을 때 확률은 0.00000000000565입니다.

다 더해봤자 정말 작네요. 애초에 30번 넘어가는 순간 대부분 확률이 정말 정말 낮으니까요.

 

따라서 드림이 치트를 쓰지 않고 41개의 엔더 진주를 얻었을 확률은 0.000000000565%라는 뜻이 됩니다.

아까도 말했지만 p-value의 임계치는 전통적으로 0.05로 잡습니다.

이 임계치에 한참 못 미치기 때문에 드림은 엔더 진주를 얻기 위해 드랍률을 올리는 치트를 썼다라는 결론을 관리팀은 도출해냅니다.

 

블레이즈 막대는?

엔더 진주 말고도 논란이 된 아이템이 하나 더 있었죠. 블레이즈 막대입니다.

원래 드랍률은 50%인데 드림만 69%(305번 중 211번)으로 측정되었습니다.

 

마찬가지로 이번에도 드림이 치트를 쓰지 않고 305번의 시도 중 211번 성공할 확률을 계산할 수 있습니다.

시도횟수는 305

성공횟수는 211

실패횟수는 94

성공확률은 0.5

실패확률도 0.5

입니다.

물론 이 계산 결과는 오직 딱 211번 성공할 확률을 구한 것이므로 p-value를 구하기 위해서는

성공횟수가 211번일 때 확률 + 212번일 때 확률 + 213번일 때 확률 + 214번일 때 확률 + ... + 304번일 때 확률 + 305번 전부 성공할 확률을 다 더해야합니다.

 

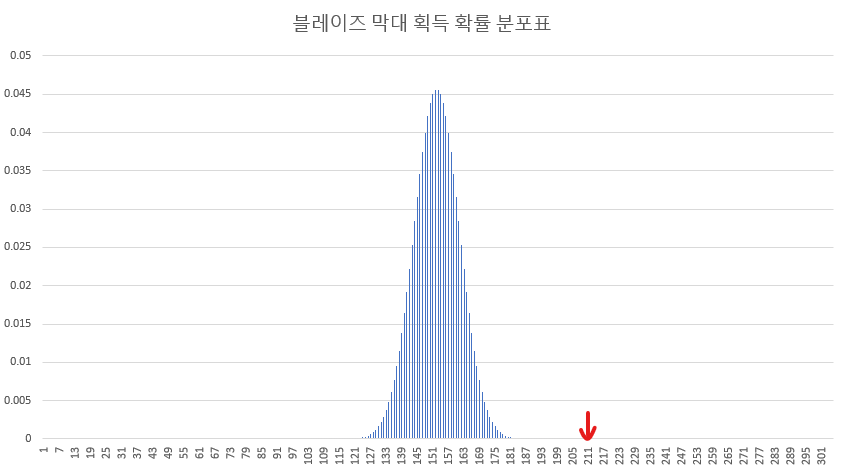
동전 던지기와 마찬가지로 블레이즈 막대도 성공 확률이 50%이기 때문에 분포표가 딱 중앙을 기준으로 대칭인 모습을 볼 수 있습니다. 상식적으로 생각해도 305번 시도하면 그 절반인 152~153번이 가장 확률이 높을 것이고, 거기서 점점 멀어질수록 확률이 낮아지겠죠.

 

그리고 이번에도 드림의 211번이라는 기록은 상식적인 수준을 아득히 벗어난 곳에 위치하고 있습니다.

211번 성공할 확률~305번 성공할 확률을 다 더한 값은 0.00000000000879 이며 이번에도 임계값 0.05에 한참 못 미칩니다.

 

엔더 진주 운이 정말 좋은 사람이 블레이즈 막대 운까지 좋을 확률?

동전과 주사위를 동시에 던졌을 때

동전은 앞면이 나오고 주사위는 4가 나올 확률은 얼마인가요?

1/2 * 1/6이므로 1/12의 확률입니다.

 

이는 p-value에서도 마찬가지입니다.

일반적으로 엔더 진주 p-value가 A이고, 블레이즈 막대 p-value가 B라면

엔더 진주와 블레이즈 막대 운이 동시에 좋을 확률은 A * B입니다.

 

하지만 확률을 곱하는 건 조심해야합니다.

두 확률 사이에 상관관계가 있을 경우엔 이렇게 섣불리 곱해선 안 됩니다.

 

아까 전의 동전 + 주사위 던지기로 가봅시다.

우리는 동전 던지기와 주사위 던지기가 서로 아무 상관이 없다는 사실을 알고 있습니다.

 

그렇기 때문에 두 경우가 동시에 일어날 확률은, 각 확률을 곱한 것과 같습니다.

 

하지만 동전 던지기가 주사위 던지기와 상관관계가 있다면요?

동전과 주사위가 일반적인 동전, 주사위가 아니라

 

이번에도 제가 나타나서 드린 (본인 주장에 따르면) 절대 공평 동전과 절대 공평 주사위라면요?

예상하시듯 이 동전과 주사위는 서로 동기화 되어있어서 동전이 앞면이 나오면 주사위는 무조건 3이 뜨게 되어있습니다.

이럴 경우엔 동전과 주사위 각각 앞면과 4가 나올 확률은 1/2, 1/6이지만 두 개를 동시에 던졌을 때 앞면 + 4가 나올 확률은 0입니다.

 

아니면 이번엔 여러분들이 역으로 주사위를 해킹(?)해서 동전이 앞면이 나오면 주사위는 무조건 4가 나오게 역으로 조작을 했다면 확률이 어떻게 되나요?

동전이 앞면이 뜨기만 하면 주사위는 발로 던져도 4가 나올테니까 동전이 앞면이 나올 확률이 결국 앞면 + 주사위 4가 나올 확률이죠? 따라서 그냥 1/2이 됩니다.

 

이렇듯 두 사건이 동시에 일어날 확률을 구한다는 것은, 단순히 두 확률을 곱한다고 다 되는 일이 아닙니다.

두 사건의 확률을 곱해도 되는 경우는 두 사건이 서로에게 전혀 영향이 없다는 보장이 있어야합니다.

 

그러면 엔더 진주와 블레이즈 막대는?

아니 2개가 상관이 있을 수가 있어?라고 생각하실 수 있지만 마인크래프트는 의외로 서로 간에 상관이 있는 확률이 정말 정말 많습니다.

 

대표적으로 예전에 국내외를 불구하고 엄청나게 유명했던 마크 다이아 찾기 방법이 있죠.

마인크래프트에서 점토와 다이아몬드 광석이 같은 랜덤 시드를 사용한다는 사실을 이용해 점토를 발견하면 다이아 위치를 거의 무조건 특정할 수 있다는 사실이 밝혀지며 마인크래프트 유저들 사이에서 매우 유명해졌습니다.

 

이뿐만 아니라 스피드러너들 사이에서는 디바인 트레블이라고 해서, 특정 좌표에 동물이 있거나, 특정 좌표에 뼛가루 블럭이 있으면 엔더 유적 좌표를 계산해내는 방법도 유명합니다.

 

즉, 마인크래프트에서는 서로 독립적이라고 생각했던 요소들이 사실은 매우 유기적으로 연결되어있는 경우가 많습니다.

 

그러면 엔더 진주와 블레이즈 막대는요?

서로 상관 관계가 없다고 할 수 있을까요?

드림의 엔더 진주 p-value가 0.00000000000565319 이고 블레이즈 막대 p-value가 0.00000000000879143라고 해서 두 값을 곱해서 0.000000000000000000000049699624이니까 드림이 치트를 안 쓰고 둘 다 저 정도 수준으로 획득할 확률은 200해 분의 1이다라는 결론을 낼 수 있을까요?

 

관리팀의 Geosquare가 그의 유튜브 영상에서 밝힌 바에 따르면 현재 스피드런 페이지 관리팀에는 Java와 마인크래프트의 랜덤에 관해 매우 해박한 지식을 가진 전문가들이 있다고 합니다.

 

그리고 그들이 밝힌 바에 따르면 물물교환에서 엔더 진주가 나오는 것은 World 랜덤을 사용하고, 블레이즈 막대는 Entity 랜덤을 사용합니다.

 

마인크래프트는 자바 언어로 짜여져있습니다.

그리고 자바로 만든 프로그램은, 디컴파일해서 소스 코드를 뜯어보기가 정말 쉽습니다.

 

물론 개발사에서 직접적으로 자신들의 코드를 푼 것도 아니고, 그들은 철저하게 감추려고 하는데 자바 언어의 특성을 이용해서 사람들이 멋대로 뜯어보는 것이기 때문에 엄밀히 따지자면 법에 걸립니다.

하지만 마인크래프트 개발팀은 마크 코드를 뜯어보는 것을 딱히 개의치 않아합니다.

 

마인크래프트의 모드 시장은 정말 큽니다. 그리고 이 모드들은 사실 전부 마인크래프트를 불법으로 뜯은 후, 제멋대로 코드를 수정해서 내놓은 개선판이라고 할 수 있습니다. 그럼에도 불구하고 마인크래프트 모드 제작자들은 그걸 기반으로 마인크래프트에 해를 끼치려고 하는 게 아니라, 오히려 마인크래프트를 재밌게 하기 위해서, 새로운 재미를 부여하기 위해서, 불편을 해소하기 위해서 모드를 제작하고, 실제로 그로 인한 유입도 많기 때문에 마인크래프트 개발자들은 이를 막지 않습니다. 실제로 모드 제작자들 중에서 마크 공식 개발팀에 영입된 인원도 많습니다.

 

아무튼, 중요한 점은 마인크래프트의 랜덤 테이블은 단풍 냄새나는 그 게임과는 다르게 자의는 아니지만 모두 투명하게 공개되어있으며, 스피드런 관리팀에는 이 분야의 전문가들이 존재하며 그들은 블레이즈 막대와 엔더 진주 사이에 연관성이 없다는 결론을 내렸습니다.

 

즉, 드림이 치트를 쓰지 않았을 확률은 아까 전에 두 값을 곱한 값인 0.0000000000000000000049699624%가 맞다는 이야기입니다.

 

이후

0.000000000000000000000049699624라는 수치는 사실 일부 요소들이 고려가 안 된 값이었습니다.

예를 들어 일반적으로 드림은 엔더 진주와 블레이즈 막대를 잘 얻은 판을 막판으로 방송을 종료하는 경향이 있기 때문에 만약 그렇지 않고 방송을 계~속 했다면 결국 엔더 진주와 블레이즈 막대 드랍율은 좀 더 떨어졌을 것이라는 점, 모든 드림 스피드런 영상을 고려한 게 아니라 일부 의심스러운 영상들만 골라서 고려했다는 점, p-hacking(이 뭔지는 모르겠지만) 등을 고려해서 다시 측정한 값은

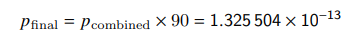
1.325504 * 10^-13 = 0.0000000000001325504로 원래 수치인 0.000000000000000000000049699624보다는 확실히 높아졌지만 그래도 임계값인 0.05엔 택도 없는(...) 수준이라 드림이 치트를 썼다는 주장엔 변함이 없었습니다.

 

그리고 이후 드림이 결국 자신이 수정된 마인크래프트 버전을 이용해 두 아이템의 드랍율을 올렸다는 점을 시인하면서 이 사건은 끝이 나게 됩니다.

 

후기

개인적으로 통계가 이렇게 흥미로울 수 있나 싶었던 스토리였습니다.

나름대로 통계학에 인연이 있음에도 불구하고 통계는 재미없다, 실용적이지 않다, 같은 데이터라도 자기 마음대로 조작하면 원하는 결론을 마음대로 도출해낼 수 있다 등의 생각을 가지고 있어 전과한 후로는 거의 통계를 손도 안 댔는데 오랜만에 이것저것 찾아보며 새로운 것도 공부하고, 예전에 배웠던 기억도 떠올리며 재밌게 보냈던 거 같습니다.

다만 0.000000000000000000000049699624 수치를 0.0000000000001325504로 수정하는 과정에서 여러가지 bias(편향)들을 다루는데 이건 PDF쪽을 봐도, 동영상을 봐도 너무 어려워서 여러 번 다시보며 이해해보려 노력해야할 것 같습니다.